[
Tugas Kuliah ] Algoritma dan Pemrograman 2 | Graf dan Pohon
Tugas
TI POLITALA Alpro 2C
Nama :
Prima Angelia Rehulina Barus
Kelas :
2C
Jurusan :
Teknik Informatika
NIM :
1801301109
Matkul :
Alpro 2 Tugas 4
Semester :
II
GRAF
DAN POHON
Pada pembahasan
kali ini, saya akan menjelaskan tentang materi graf dan pohon khususnya materi graf
dan pohon dengan algoritma djikstra dan kruskal. Materi ini berdasarkan hasil
diskusi kelompok dengan kasus rumah makan terdekat di Pelaihari dengan
algoritma djikstra dan kruskal.
A.
Pengertian Graf
Sebuah
graf G didefinisikan sebagai pasangan himpunan (V,E) , dengan V adalah himpunan
tak kosong yang terdiri dari simpul-simpul (vertices) atau titik pada G.
Sedangkan E adalah himpunan rusuk (edge) atau sisi pada G yang menghubungkan
sepasang simpul atau titik. Himpunan simpul atau titik pada G dinotasikan
sebagai V, dan himpunan rusuk atau sisi pada G dinotasikan sebagai E. Jadi
G=(V, E)
Berdasarkan ada tidaknya gelang atau sisi ganda pada
suatu graph, maka graph digolongkan menjadi dua jenis:
1.
Graph sederhana (simple graph).
Graf yang tidak mempunyai
gelang atau loop maupun sisi ganda.
2.
Graph tak-sederhana (unsimple-graph).
Graf yang
mempunyai gelang atau loop maupun sisi ganda.
Berdasarkan
jumlah simpul pada suatu graph, maka secara umum graph dapat digolongkan
menjadi dua jenis:
1. Graph
berhingga (limited graph)
2. Graph
tak-berhingga (unlimited graph)
Berdasarkan orientasi arah
pada sisi, maka secara umum graph
dibedakan atas 2 jenis:
1. Graph
tak-berarah (undirected graph)
Graph yang sisinya tidak
mempunyai orientasi arah atau panah disebut graph tak-berarah.
2. Graph
berarah (directed graph atau digraph)
Graph yang setiap sisinya
diberikan orientasi arah atau panah disebut sebagai graph berarah.
Algoritma Graf
Algoritma Graf yang
dibahas dalam laporan ini ada 2 yaitu :
a)
Algoritma Dijkstra (Pencarian Jalur Terpendek)
Algoritma
ini bertujuan untuk menemukan jalur terpendek berdasarkan bobot terkecil dari
satu titik ke titik lainnya. Misalkan titik mengambarkan gedung dan garis
menggambarkan jalan, maka algoritma Dijkstra melakukan kalkulasiatau total terhadap semua kemungkinan bobot terkecil dari
setiap titik yang dilalui.
Pertama-tama
tentukan titik mana yang akan menjadi node awal, lalu beri
bobot jarak pada node pertama ke node terdekat
satu per satu, Dijkstra akan melakukan pengembangan pencarian dari satu titik ke
titik lain dan ke titik selanjutnya tahap demi tahap. Inilah urutan logika dari
algoritma Dijkstra:
1. Beri
nilai bobot (jarak) untuk setiap titik ke titik lainnya, lalu set nilai 0 pada node awal
dan nilai tak hingga terhadap node lain (belum terisi).
2. Set
semua node “Belum terjamah” dan set node awal
sebagai “Node keberangkatan”.
3.Dari node keberangkatan,
pertimbangkan node tetangga yang belum terjamah dan hitung
jaraknya dari titik keberangkatan. Sebagai contoh, jika titik keberangkatan A
ke B memiliki bobot jarak 6 dan dari B ke node C berjarak 2,
maka jarak ke C melewati B menjadi 6+2=8. Jika jarak ini lebih kecil dari jarak
sebelumnya (yang telah terekam sebelumnya) hapus data lama, simpan ulang data
jarak dengan jarak yang baru.
4. Saat kita
selesai mempertimbangkan setiap jarak terhadap node tetangga,
tandai node yang telah terjamah sebagai “Node terjamah”. Node terjamah
tidak akan pernah di cek kembali, jarak yang disimpan adalah jarak terakhir dan
yang paling minimal bobotnya.
5. Set “Node belum
terjamah” dengan jarak terkecil (dari node keberangkatan)
sebagai “Node Keberangkatan” selanjutnya dan lanjutkan dengan
kembali ke step 3.
2. Algoritma
Kruskal
Algoritma
Kruskal adalah sebuah algoritma dalam teori graf yang mencari sebuah minimum
tree untuk sebuah graf berbobot yang terhubung. Jika grafik tidak terhubung,
maka menemukan hutan rentang minimum (pohon rentan minimum untuk setiap
komponen terhubung). Dasar pembentukan algoritma Kruskal berasal dari analogi
glowing forest. Glowing forest maksudnya adalah untuk membentuk pohon merentang
minimum T dari graf G adalah dengan cara mengambil satu persatu sisi dari graf
G dan memasukkannya ke dalam pohon yang telah terbentuk sebelumnya. Seiring
dengan berjalannya iterasi untuk setiap sisi, maka forest akan memiliki pohon
yang semakain sedikit. Algoritma Kruskal akan terus menambah sisi-sisi kedalam
hutan yang sesuai hingga akhirnya tidak akan ada lagi forest, melainkan hanyalah
sebuah pohon yang merentang minimum.
Secara umum
Algoritma Kruskal ditulis:
1.
T
masih kosong
2.
Pilih
sisi (i, j) dengan bobot minimum
3.
Pilih
sisi (i, j) dengan bobot minimum yang berikutnya yang tidak membentuk cycle di
T, tambahkan (i,j) ke T
4.
Ulangi
langkah 3 sebanyak (n-2) kali
5.
Total
langkah (n-1) kali
Karakteristik dari Algoritma Kruskal :
a.Sifat dari Algoritma Kruskal
1. Bekerja tidak hanya dengan grafik
diarahkan.
2. Bekerja dengan bobot dan tidak grafik
tertimbang. Tapi yang lebih menarik, apabila tepi yang berbobot.
3. Kruskal adalah jenis algoritma yang
menghasilkan solusi optimal MST.
Langkah-Langkah Algoritma Kruskal
Langkah-langkah algoritma Kruskal adalah
sebagai berikut:
1. Atur tepi berat: pling berat pertama
dan terberat terakhir.
2. Pilih yang ringan tidak diperiksa tapi
dari diagram.
3. Tambahkan tepi memilih ini ke pohon,
hanya jika hal itu tidak membuat siklus.
4. Menghentikan proses kapanpun n-1 tapi
lebih ditambahkan kepohon.
B.
Pengertian Pohon
Pohon (tree) adalah merupakan
graf yang tak berarah terhubung yang tidak memuat sirkuit sederhana. pohon
adalah suatu graph yang banyak vertexnya sama dengan n (n>1), jika :
~ Graph tersebut
tidak mempunyai lingkar (cycle free) dan banyaknya rusuk (n-1).
~ Graph tersebut
terhubung .
Hutan ( forest )
merupakan kumpulan pohon yang saling lepas. Dengan kata lain, hutan merupakan
graf tidak terhubung yang tidak mengandung sirkuit.
Berikut adalah beberapa sifat pohon :
1. Misalkan G merupakan suatu graf
dengan n buah simpul dan tepat n – 1 buah sisi.
2. Jika G tidak mempunyai sirkuit
maka G merupakan pohon.
3. Suatu pohon dengan n buah simpul mempunyai
n – 1 buah sisi.
4. Setiap pasang simpul di dalam
suatu pohon terhubung dengan lintasan tunggal.
5. Misalkan G adalah graf sederhana
dengan jumlah simpul n,jika G tidak mengandung sirkuit maka penambahan satu
sisi pada graf hanya akan membuat satu sirkuit.
C.
Permasalahan
Permasalahan yang
terdapat pada laporan ini adalah sebagai berikut:
1.
Membuat sebuah pembahasan tentang graf dan
pohon serta algoritma djikstra dan kruskal.
2.
Membuat sebuah program mencari jalur
terpendek antar rumah makan terdekat di Pelaihari menggunakan algoritma
djikstra dan kruskal.
D. Penjelasan
Kasus
Kasus
yang diambil dalam laporan ini adalah kasus rumah makan terdekat di pelaihari.
Disini diambil beberapa rumah makan ada sekitar 10 rumah makan. Dari 10 rumah
makan tersebut diukur jaraknya di google map untuk memuat grafnya. Setelah itu
dibuat jarak satu persatu rumah makan untuk membuat matriks berbobotnya.
a) Map
b) Graf
Djikstra dan Kruskal
c) Matriks
Djikstra
d) Matriks
Kruskal
e) Codingan
Algoritma Djikstra
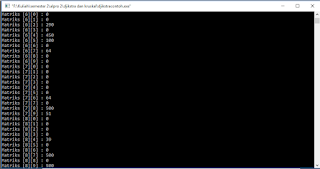
Hasil
Running Djikstra
f) Codingan
Algoritma Kruskal
Hasil
Running Kruskal
Sekian penjelasan
dari saya tentang materi graf dan pohon khususnya materi graf dan pohon dengan
algoritma djikstra dan kruskal. Semoga bermanfaat.
Daftar pustaka
Rifanti, Marina Utti. 2017. “PEMILIHAN RUTE TERBAIK
MENGGUNAKAN ALGORITMA DIJKSTRA UNTUK MENGURANGI KEMACETAN LALU LINTAS DI
PURWOKERTO (BEST ROUTE SELECTION USE DIJKSTRA ALGORITHM TO REDUCE TRAFFIC
CONGESTION IN PURWOKERTO)”. Diakses pada tanggal 25 Mei 2019 pukul 09.30 WITA
dari https://www.researchgate.net/publication/325059321_Pemilihan_Rute_Terbaik_Menggunakan_Algoritma_Dijkstra_Untuk_Mengurangi_Kemacetan_Lalu_Lintas_di_Purwokerto/download
Amrullah. 2018. “APLIKASI GRAF POHON PADA ALGORITMA
HUFFMAN”. Diakses pada tanggal 25 Mei 2019 pukul 10.45 WITA dari
https://www.researchgate.net/publication/322423546




























0 komentar:
Posting Komentar